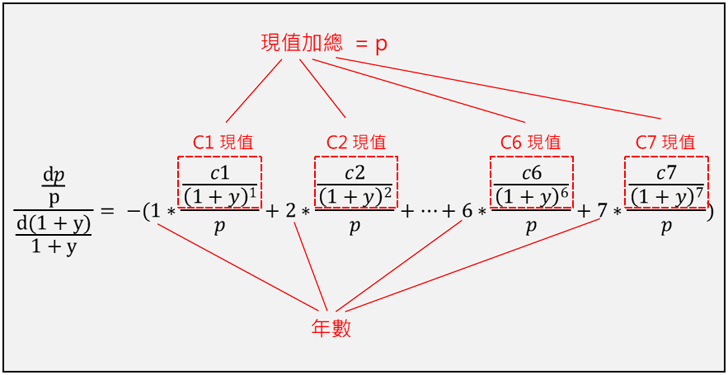
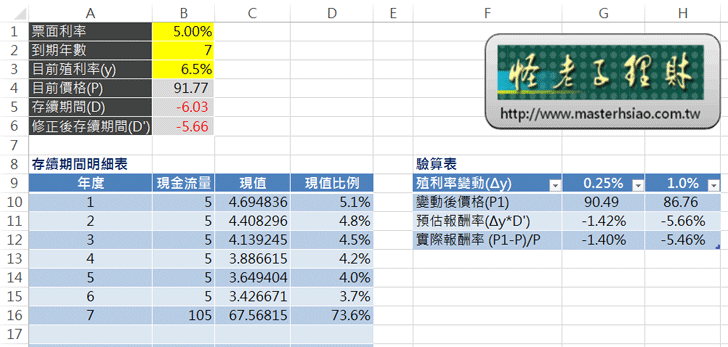
一、利率、債券
「利率是貨幣的成本,債券是股票的替代品」
長天期公債殖利率與通膨預期較為相關,而短天期公債殖利率較易受到聯邦基金利率預期的影響。
利率
「利率」是由中央銀行決定,在美國當然是由美國聯邦銀行FED,在台灣則是中央銀行控制。套句科老的話「中央銀行:利率的獨裁者」。各國目前的利率都非常的低,有些國家的利率更低到零。全球央行均刻意的壓低利率(除了俄羅斯及巴西之外),以創造刺激通膨的環境。在這種長期低利率下,造就全球的資金氾濫、熱錢亂竄。
債券
「債券」的長期利率不是由中央銀行決定,大致上由市場決定(不考慮QE購債的間接影響)。美國10年期公債殖利率普遍被市場認為是零風險利率。債券的利率越高,對股票的壓力越大。所有的投資者,無論是大型保險公司或退休基金的基金經理,還是小儲戶,都必須選擇一種投資方式,選擇股票,還是債券?(因為保有現金的定存利率,通常會被通膨所吞噬)
如果債券利率高於通貨膨脹率和股票紅利,大家就會選擇債券。如果長期債券利率低,投資者願冒更大的風險,轉向投資股票。因此,債券市場利率愈高,可供股票市場利用的資金愈少。反之,債券市場利率愈低,可供股票市場利用的資金愈多。套句科老的話「債券:股票的競爭者」。
二、金融市場報酬的四個時期
墨基爾在《漫步華爾街》一書中,為了衡量股票及債券的報酬,將金融市場分成四個時期討論:

以下比較時期二、時期三、時期四,美國標準普爾500指數與10年期公債殖利率的比較分析。
(一)1969~1981年 焦慮時期

事件一:60年代末期,美國涉入越南戰爭,產生「需求拉動」型通貨膨脹(太多的金錢追逐太少的商品)。
事件二:1973年~1974年的石油和食物危機,石油輸出國家組織聯手造成石油短缺。
事件三:1978年~1979年經濟部門的過度需求、薪資與勞動成本一起上漲。
(以上摘錄自《漫步華爾街》)
事件二:1973年~1974年的石油和食物危機,石油輸出國家組織聯手造成石油短缺。
事件三:1978年~1979年經濟部門的過度需求、薪資與勞動成本一起上漲。
(以上摘錄自《漫步華爾街》)
股票的年報酬率只有5.6%。

1969年,10年期公債殖利率平均約6%,但通膨率以二位數的成長,誰願意買殖利率僅6%的債券?要賣就要賠本出售,新投資人的收益才能敵過更高的通貨膨脹率。因此,債券的風險溢酬因計入升高的價格波動而增加。到了1981年債券殖利率飆升到15.4%(公債價格崩跌!)。
本益比下滑

70年代股票價格下跌的主要原因,在於投資人對於盈餘和股利的評價,也就是他們願意為每一塊錢盈餘和股利的金額報酬下降所致。1969年到1981年期間,標普500指數的本益比下滑了三分之二,更有10多年的時間本益比在10倍以下。本益比的下跌是70年代股市投資人報酬不佳的原因,是股票未能反應公司盈餘和股利成長。
(以上摘錄自《漫步華爾街》)
(以上摘錄自《漫步華爾街》)

(二)1982~2000年 繁榮時期

1982年到2000年,美國標普500指數的漲幅驚人。1982年標普500指數的低點102.2點,2000年標普500指數的高點1553點,期間漲幅超過14倍。股票的年化報酬率有18.3%。
股市的繁榮時期,美國10年期公債利率長期下跌(價格上升)如圖:

1982年為美債大多頭的開端(債券利率下跌,代表債券的價格上升)。1981年9月,美國10年期公債殖利率來到歷史高點15.84%,到了1998年9月來到4.01%。繁榮時期,債券的年化報酬率有13.6%,僅次於股票的報酬率。
「繁榮時期」的報酬率比較:股票(18.3%) > 債券(13.6%) > 通膨(3.3%)。1982年到2000年初,是投資於金融資產千載難逢的時機,這也應該是人類史上,創造最多富人的年代!

從初任薪資的成長,看出台灣經濟奇蹟,也是發生在這個繁榮時期,初任薪資成長了四倍。這個期間正是我的求學時代(小學到研究所),進入職場後,薪資就進入了停滯期。
1987年的黑色星期一 (繁榮時期的小插曲)
1987年10月19日(星期一)的股災。當日全球股市在紐約道瓊斯工業平均指數帶頭暴跌下全面下瀉,引發金融市場恐慌。
1987年10月20日早上10時,香港股市開市,受紐約影響恐慌性下瀉120點,中午收市下跌235點,全日收市共下跌420.81點,收盤3362.39 (超過 10%)。受香港暴跌影響,各亞太地區股市全面下瀉,效應並如骨牌般隨各時區陸續開市擴展至歐洲市場,並最終繞地球一圈回到紐約:道瓊斯工業平均指數在10月19日大幅下跌508點 (逾 20%)。
整個1987年10月的跌幅,香港全月下跌 45.8%、雪梨全月下跌 41.8%、台灣全月下跌39%、倫敦全月下跌 26.4%、紐約全月下跌 22.6%。股災後很多人提出不同的理論,主要認為股災成因包括:程式交易、股價過高、市場上流動資金不足和羊群心理。
美債殖利率最高10.23%(1987年10月16日),隨後資金湧入債券避險,美債殖利率下滑。隔年2月,公債殖利率在8.11%止穩。
1998~2000年 網路破沫 (繁榮時期的完結篇)

棕色線(右軸)為美國10年期公債利率(代表長債利率);綠色線(左軸)為S&P500指數(代表股市)
1998/10/05~2000/01/20股市進入最後衝刺,標普500指數由988飆到1445,僅14個月(漲幅50%)。
2000/01/20美國10年期公債利率反彈到高點6.79%,債券的資金流入股市追逐股價。
2000/03/24標普500指數飆漲到1527,隨後就爆發了「網路泡沫」。
2000/01/20美國10年期公債利率反彈到高點6.79%,債券的資金流入股市追逐股價。
2000/03/24標普500指數飆漲到1527,隨後就爆發了「網路泡沫」。
泡沫前特徵:債券殖利率上揚(債券價格下跌),醞釀股市狂飆泡沫。
泡沫破滅:債券利率下滑(債券價格上升),顯示資金持續由股市流向債市。
泡沫破滅:債券利率下滑(債券價格上升),顯示資金持續由股市流向債市。

(三)2000~2009年 覺醒時期
緊隨著繁榮時代而來的,是股市有史以來最糟糕的十年之一。起先是網路泡沫,後有金融海嘯。

2000年的網路泡沫,標普500指數由1527跌到2002年10月的768(跌幅50%)
2008年的金融海嘯,標普500指數由1576跌到2009年3月的666(跌幅58%)
2008年的金融海嘯,標普500指數由1576跌到2009年3月的666(跌幅58%)
2007-2008年 金融海嘯 (覺醒時期的下半場)
金融海嘯的債券與股市的互動關係,也出現類似網路泡沫的過程。

紅色線(右軸)為美國10年期公債利率(代表長債利率);綠色線(左軸)為S&P500指數(代表股市)
2004年到2007年是美股的大多頭,期間美債殖利率由3%緩步上升到5%。
2006/06/14~2007/06/12股市進入最後衝刺,標普500指數由1219飆到1493,僅13個月(漲幅22%)。
2007/06/12美債殖利率來到相對高點5.26%,債券的資金流入股市追逐股價。
2007/10/09標普500指數飆漲到1565,隨後就發生了「金融海嘯」。
2006/06/14~2007/06/12股市進入最後衝刺,標普500指數由1219飆到1493,僅13個月(漲幅22%)。
2007/06/12美債殖利率來到相對高點5.26%,債券的資金流入股市追逐股價。
2007/10/09標普500指數飆漲到1565,隨後就發生了「金融海嘯」。
「金融海嘯」與「網路泡沫」的前、後特徵相似:
泡沫前特徵:債券殖利率上揚(債券價格下跌),醞釀股市狂飆泡沫。
泡沫破滅,債券利率下滑(債券價格上升),顯示資金持續由股市流向債市。
泡沫前特徵:債券殖利率上揚(債券價格下跌),醞釀股市狂飆泡沫。
泡沫破滅,債券利率下滑(債券價格上升),顯示資金持續由股市流向債市。

網路泡沫
2000/03/24 美國標普500來到歷史高點 1527點。
2000/01/20 美國10年期公債殖利率來到波段高點 6.80%,領先股市 2個月。
2000/01/20 美國10年期公債殖利率來到波段高點 6.80%,領先股市 2個月。
金融海嘯
2007/10/09 美國標普500再創歷史高點 1565點,
2007/06/12 美國10年期公債殖利率來到波段高點 5.26%,領先股市 4個月。
2007/06/12 美國10年期公債殖利率來到波段高點 5.26%,領先股市 4個月。

負斜率殖利率曲線 (網路泡沫與金融海嘯)

債市有各種期別的債券交易,正常情況下,到期日越短的債券,利率(票面利率與殖利率)越低。反之,到期日越長的債券,利率越高。這是由於投資人持有債券期間越長,未來碰上利率變動的機率也越高,也就是不確定風險較高,為了彌補更高的不確定風險,特別是長天期債券投資人會要求更高的「風險貼水」、「風險溢價」,也就是會要求更高的利率,以貼補未來可能的升息風險。
一旦短天期的公債殖利率,高過長天期的公債殖利率,就是所謂的「負斜率曲線」。2000年底(網路泡沫化之前)、2007年(金融海嘯前)都曾經發生負斜率的現象,且持續一段時間。這代表資金從短債流出,點燃股市最後的煙火秀。
三、2009-2014年 (印鈔救世的年代)
美國三輪QE啟動資金行情

QE3實施不久,美國標普500指數已突破金融海嘯前的高點,且持續的創新高。
QE期間,美國10年期公債殖利率的變化

美國10年期公債殖利率,從2007年金融海嘯的高點5.26%,下滑到2012年7月的歷史低點1.43%,這應該是美國聯准會所樂見的結果,貨幣寬鬆政策壓低了利率,也壓低了公債殖利率,藉此刺激實體經濟的需求,期望降低失業率。
然而,QE3實施(2012年9月)後,美國10年期公債利率不跌反漲,公債利率上揚了一倍(2014年1月,3.02%),資金由債市流入股市。這種資金的流向使得標普500,在此期間由1266點(2012/06)一路飆漲到1985(2014/07),漲幅高達57%。
2014年,隨著美國量化寬鬆政策逐月的減少購債規模,資金回流美國,造成美元升值、股市持續上漲,10年期公債殖利率越走越低。
近期美國10年期公債殖利率

2015年1月30日10年期公債殖利率下挫至1.65%,非常的逼近歷史低點1.43%。
目前美國各期公債殖利率

目前短天期的公債殖利率維持很低的水位,要發生負斜率曲線的機率不高。但近一個月,2年公債殖利率持續上升,但距離10年期公債殖利率仍有一小段距離。未來若發生短天期公債殖利率往上升,10年期公債殖利率持續向下,並出現負斜率曲線,股市就要特別小心了。
結論:
- 美國10年期公債殖利率會領先股市創高,隨後債券殖利率與股市會同步下挫。
- 負斜率殖利率曲線(短債利率高於長債利率),若持續一段時間,是股市頭部的重要特徵之一。
《談股論經》授權轉載
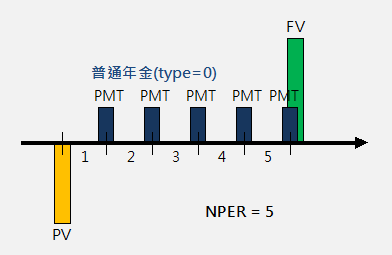

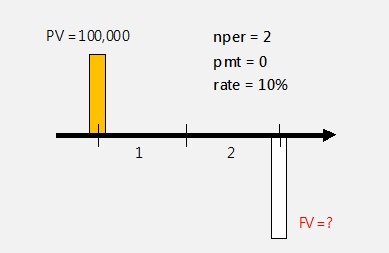
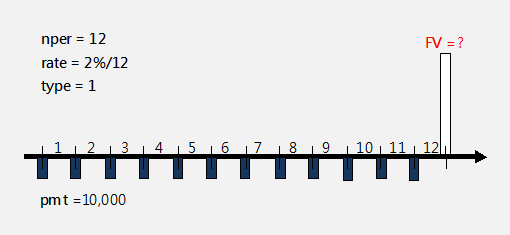
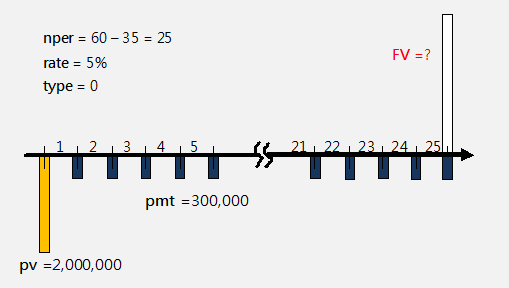
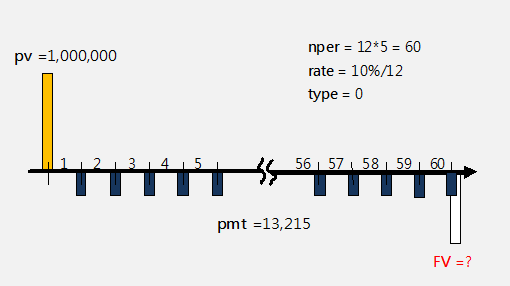
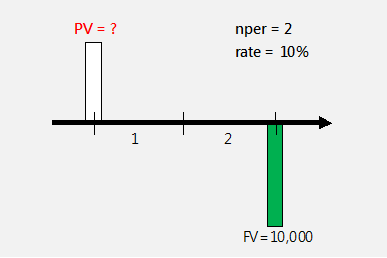
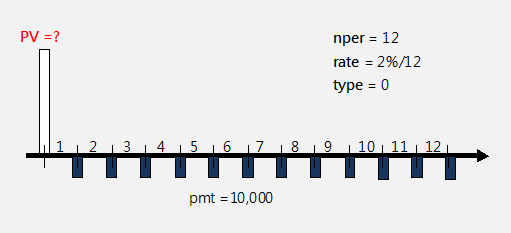
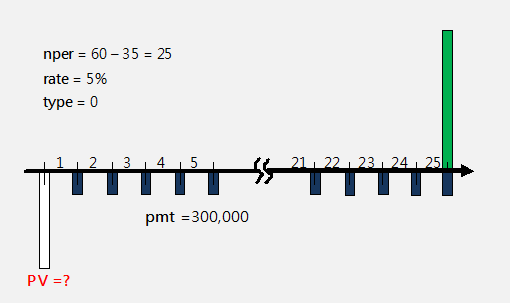
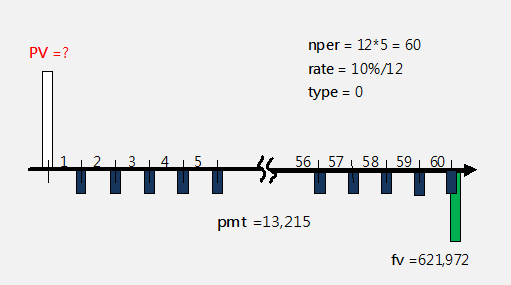
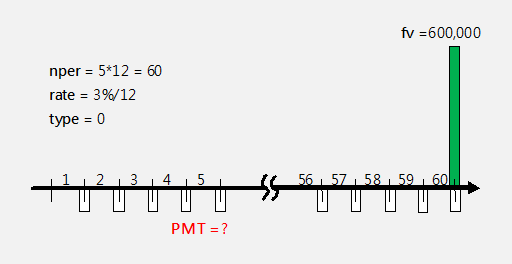
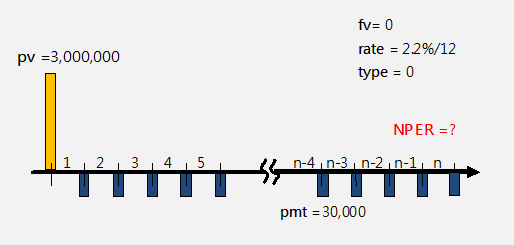
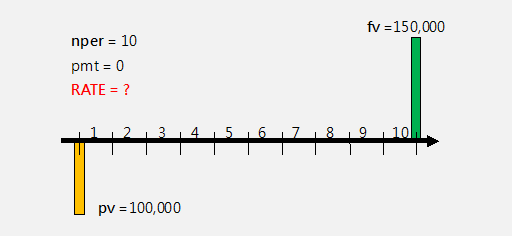
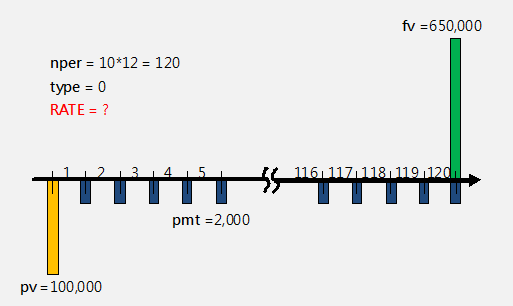
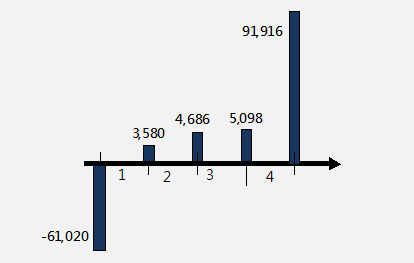
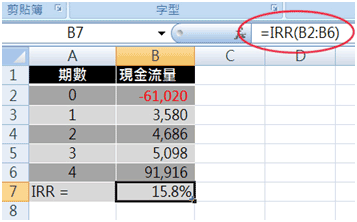





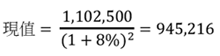
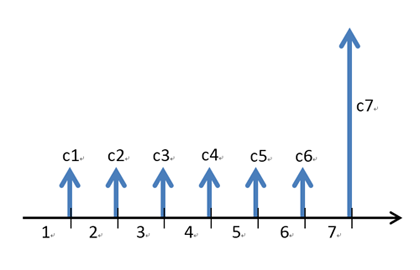
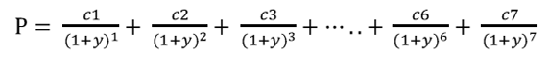 -----公式一
-----公式一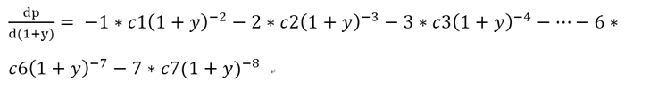
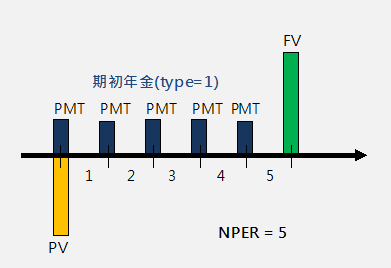
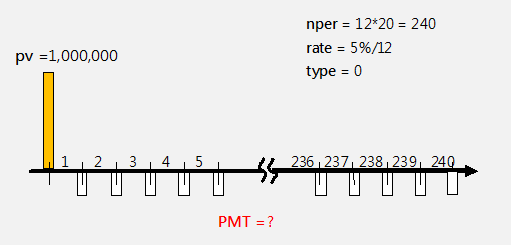
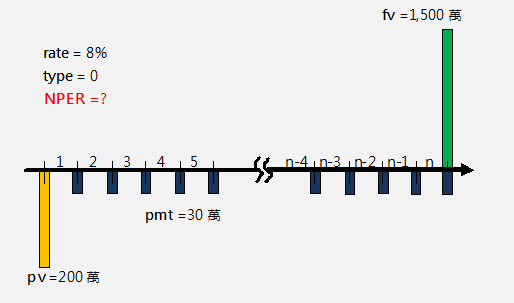
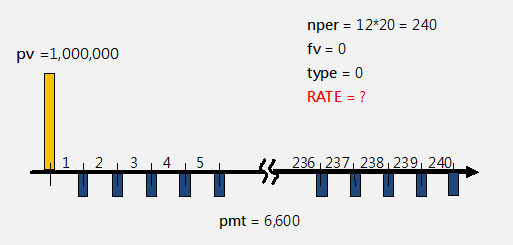
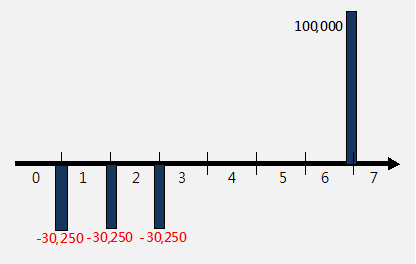
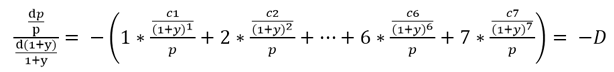 -----公式二
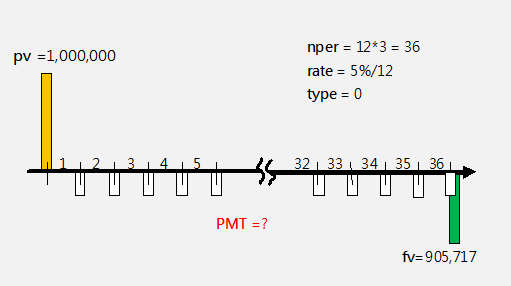
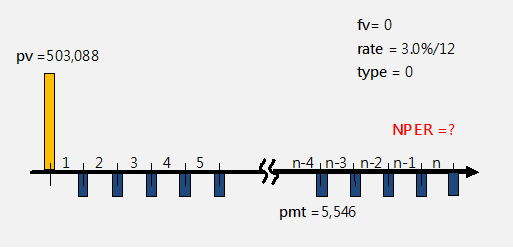
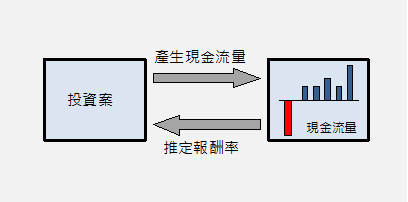
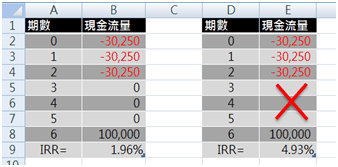
-----公式二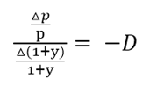 -----公式三
-----公式三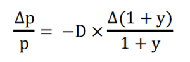
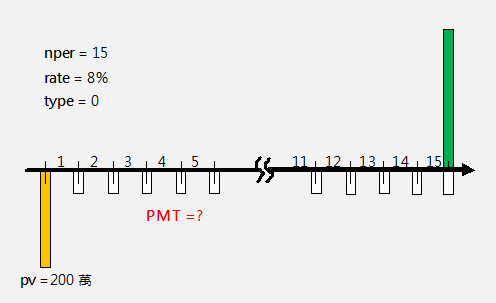
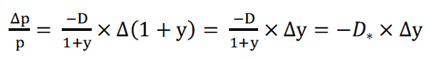 -----公式四
-----公式四